矩阵变换与投影矩阵变换与投影

项目地址：https://github.com/OmegaZhou/SimpleRenderer

矩阵变换

旋转

• 对于一个三维的坐标点来说，我们可以通过如下矩阵令该点绕某一个坐标轴旋转，当然想绕任意轴旋转也是可以做到的，不过旋转矩阵较为复杂，在本项目中，我仅令矩阵沿三个坐标轴进行旋转

缩放

• 我们仅需使用一个对角阵就可以完成缩放操作，元素(i,i)就代表坐标的第i项的缩放比例

平移

• 由于仅仅使用三维矩阵进行变换的话，我们无法完成平移操作

• 这里我们引入第四维w，并且我们有如下定义(x,y,z,1)和(xw,yw,zw,w)表示的是同一个坐标，即三维空间中的坐标(x,y,z)，这样我们就可以用一个四维向量来描述一个平移变换了

• 这里对于坐标(x,y,z,1)，我们若要获得坐标(x+a,y+b,z+c,1)，我们只需使用如下的平移矩阵即可
  

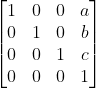
复杂变换

• 对于若干个矩阵变换$A_0,A_1,A_2...$，我们只需按照变换顺序依次左乘得到新的矩阵$B=...A_2A_1A_0$，即得到复杂变换B，效果等价于执行这若干个矩阵变换

法向量变换

• 对于一个坐标点来说，执行完坐标变换后，不能保证原法向量仍与切向量垂直，因此我们得同时对法向量进行相应变换，设切向量为A，法向量为B，坐标点的变换矩阵为C，设B的变换矩阵为D，在对坐标点执行C变换后，显然切向量A就变换为CA
• 首先由定义可知A^TB=0，为保证变换后仍保证该性质，即(CA)^T(DB)=AC^TDB=0
• 因此我们令D=(C^T)^{-1}，即可使得(CA)^T(DB)=0

投影

• 为了将三维空间的点映射到二维平面中，我们就得对空间的每个坐标点进行投影操作

正交投影

• 设l<=x<=r,b<=y<=t,n<=z<=f，为了方便之后的操作，我们需要进行一个简单的映射操作令[l,r]->[-1,1],[b,t]->[-1,1],[n,f]->[-1,1]，变换矩阵即为
  

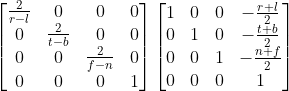
• 正交投影可视为在空间中使用平行光去照射物体，最终将得到的坐标将其映射到二维平面时，保持x轴和y轴坐标不变即可

透视投影

• 透视投影则是符合人眼的视觉效果，近大远小

• 其主要思路是根据摄像机视场角（FOV）从摄像机投射出若干射线，形成视锥，根据预先设定好的最近可视距离（n）和最远可视距离（f），截取出可视的区域，将该区域压缩成一个标准正方体(canonical cube, [-1,1]^3)

• 设点的坐标为(x,y,z,1)，按照近大远小的思路，根据z轴对点进行压缩，即得到(nx/z,ny/z,?,1)，该点与(nx,ny,?,z)等价，同时，对于最近和最近的可视平面来说，其z值保持不变，同时考虑到对z轴变换时，仅与z相关与x，y轴无关，因此设z轴对应的变换为(0,0,A,B)即
  (0,0,A,B)(0,0,n,1)^T=(0,0,n^2,n)^T
  (0,0,A,B)(0,0,f,1)^T=(0,0,f^2,f)^T

• 得到A=n+f,B=-nf

• 最终可得到透视矩阵
  

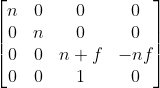
• 最后将得到的矩阵执行一次正交投影操作，即可得到标准正方体

视口变换

• 为了将图像显示在屏幕上，我们还需对得到的标准正方体进行视口变换
• 令x=(x + 1) width / 2,y=(y + 1) height/ 2，我们可以获得对应屏幕上的横纵坐标
• 通过f1=(f-n)/2,f2=(f+n)/2,z=z*f1+f2，我们可以将z轴变换至视锥的可视范围内