线性BVH树并行构建方法

背景

• 传统BVH树采用递归的方式实现，不利于并行实现

前置步骤

构造一个排序好的叶子节点序列

目的

• 有利于合并操作，由于叶节点已经排序完毕，只需合并相邻叶节点或非叶节点即可构造出新的父节点
• 不需要重新进行排序操作来构造划分，从而使得构建无法并行化

要求

• 相邻叶子节点要尽可能靠近

做法

• 每一个AABB提供一个point（这里采用包围盒重心）
• 将该point坐标转换为Morton Code
• 根据Morton Code进行排序

原理

• 相当于将空间划分成一个个体素，每一个Morton Code代表一个体素
• 可类比于2D空间中的Z型曲线，大部分相临编码的体素在空间中相邻
• 可通过前缀将若干个小体素合并成大体素，符合BVH树的合并需求

缺点

• 该划分方式假定绝大部分三角面片足够小，仅存在于point附近的几个体素内
• 对于部分大的三角面片，查询效果较差，但依旧能够保证鲁棒性

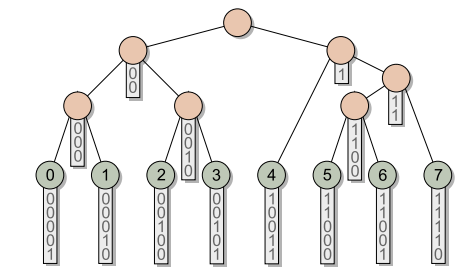
BVH树合并标准

• 根据前缀和进行合并，有相同前缀和的的节点属于同一个非叶节点
• 从底向上前缀和逐渐变小，从而构建出树的层级、
• 如图所示

构建算法

伪代码

概念解释

• 叶子节点

  • 每一个物体作为最小单元存储在叶子节点中
  • 同时存储物体的包围盒信息，包括Morton Code

• 非叶节点

  • 通过合并叶子节点/非叶节点得到
  • 存储合并后的包围盒信息，包括Morton Code前缀

• 节点存储

  • 使用两个数组分别存储叶子节点和非叶节点
  • 数组L：存储叶子节点的数组
  • 数组I：存储非叶节点的数组
  • N：叶子节点数组大小，N-1：非叶节点数组大小

• 下标

  • 叶子节点下标：代表在L中的位置
  • 非叶节点下标
  • 代表在I中位置
  • 根节点下标=0
  • 若该非叶节点为其父节点的左孩子，则非叶节点下标=所包含最右端叶子节点的下标
  • 若该非叶节点为其父节点的右孩子，则非叶节点下标=所包含最左端叶子节点的下标

• δ(i, j)：

  • 返回L[i]和L[j]节点的Morton Code的最长公共前缀长度

• 分割位置γ

  • 若非叶节点K所包含的叶节点下标范围为[l,r]
  • 则其左右子树包含的叶节点下标范围分别为[l,γ]，[γ+1,r]

算法解析

// 该算法的目的是找到I[i]的左右子树，从而将其合并
for each internal node with index i ∈ [0,n n 2] in parallel
    // Determine direction of the range (+1 or -1)
    // 判断方向，若i为左孩子，L[i]为I[i]最右元素，则d=1，若i为右孩子，L[i]为I[i]最左元素，d=-1
    d ← sign(δ(i,i+1) ) δ(i,i i 1))
    // Compute upper bound for the length of the range
    // 计算前缀长度的下界，由于i-d必然不属于i子树，假设i子树的前缀为δ_i，因此δ(i,i-d)<δ_i
    δ_min ← δ(i,i-d)
    l_max ← 2
    // 由于i子树内的前缀长度必然大于δ_min，因此若δ(i,i+lmax*d)<=δ_min,则i+lmax*d不在i子树中
    // 因此该循环找到一个下界，即i子树的另一个端点必然属于[i,i+lmax*d)
    while δ(i,i+lmax*d) > δ_min do
        lmax ← lmax*2
    // Find the other end using binary search
    // 使用二分查找找到I[i]的另一个端点j
    l ← 0
    for t ← {lmax/2,lmax/4,...,1} do
        if δ(i,i+ (l +t)· d) > δmin then
            l ← l +t
    j ← i+l · d
    // Find the split position using binary search
    // 接下来查找I[i]的划分位置γ
    // 同样使用二分查找的方式查找，这里由于方向问题，最后还要进行处理一下
    // 若d=1，则查找到的结果是γ，反之则是γ+1，故此时需要再减去1
    δnode ← δ(i, j)
    s ← 0
    for t ← {l/2, l/4,...,1} do
        if δ(i,i+ (s+t)· d) > δnode then
            s ← s+t
    γ ← i+s· d +min(d,0)
    // Output child pointers
    // 判断子节点属于I数组还是L数组
    if min(i, j) = γ then left ← Lγ else left ← Iγ
    if max(i, j) = γ+1 then right ← Lγ+1 else right ← Iγ+1
    // 合并结果
    Ii ← (left,right)
end for

后置步骤

合并AABB

• 并行从所有叶子节点出发进行迭代更新
• 为每个非叶节点设置标记位
• 每次访问到非叶节点，采用原子操作将其递增，若访问非叶节点两次则合并该节点的两个子节点（由于每个非叶节点有且只有两个子节点，因此这样可以保证子节点的aabb都已更新完毕），反之则结束迭代
• 继续迭代该节点的父节点
• 缺点：每次迭代后，就有一半线程结束迭代闲置，但该操作耗时不大，这样的损失是可以接受的

查询

• 可采用BFS或DFS的方式进行查询，若查到某一个包围盒相交，则继续查询其子节点是否相交，直至查询到叶子节点

参考文献

• Maximizing Parallelism in the Construction of BVHs, Octrees, and k-d Trees